Bachelor Thesis: Comparison of Convex Approximation Schemes for Modifier Adaptation with Quadratic Approximation
- Thesis offer
Introduction
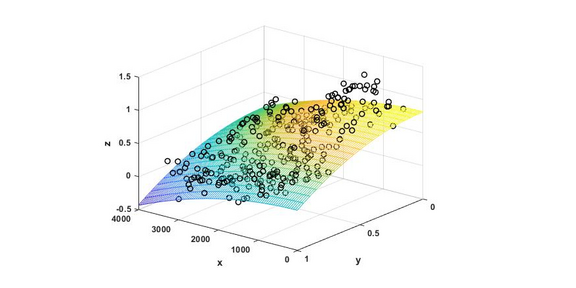
Real-time optimisation [1] is a high-level model-based control technique in which the operating conditions of a chemical plant or process are optimized. Thereby, the inevitable plant-model mismatch needs to be addressed. In modifier adaptation schemes [2-3], the cost and constraint function of optimization problem are corrected based on available measurement data. Gao et al. [4] proposed “Modifier Adaptation with Quadratic Approximation” (MAWQA), in which quadratic approximations (QA) are used to estimate the necessary plant gradients. An important criterion for the convergence to the optimal set-points is the use of “adequate” models [5-6]. In MAWQA, this can be achieved by the approximation of convex quadratic functions. In this thesis, different schemes for the convex approximations of QAs for MAWQA shall be investigated and compared.
Objectives
- Review of existing literature
- Investigation of different convex approximation schemes for quadratic functions
- Implementation into modifier adaptation with quadratic approximation
- Comparative simulation study
Prerequisites
- Programming skills (MATLAB, Python)
- Interest in process performance optimisation
- Interest in advanced process control and optimisation
Literature
[1] D. Müller et al., “Real-Time Optimization in the Chemical Processing Industry,” Chemie-Ingenieur-Technik, vol. 89, no. 11, pp. 1464–1470, 2017, doi: 10.1002/cite.201700033.
[2] W. Gao and S. Engell, “Iterative set-point optimization of batch chromatography,” Comput. Chem. Eng., vol. 29, no. 6 SPEC. ISS., pp. 1401–1409, 2005, doi: 10.1016/j.compchemeng.2005.02.035.
[3] A. Marchetti, B. Chachuat, and D. Bonvin, “Modifier-Adaptation Methodology for Real-Time Optimization,” pp. 6022–6033, 2009.
[4] W. Gao, S. Wenzel, and S. Engell, “A reliable modifier-adaptation strategy for real-time optimization,” Comput. Chem. Eng., vol. 91, pp. 318–328, 2016, doi: 10.1016/j.compchemeng.2016.03.019.
[5] G. François and D. Bonvin, “Use of convex model approximations for real-time optimization via modifier adaptation,” Ind. Eng. Chem. Res., vol. 52, no. 33, pp. 11614–11625, 2013, doi: 10.1021/ie3032372.
[6] A. R. Gottu Mukkula and S. Engell, “Guaranteed Model Adequacy for Modifier Adaptation With Quadratic Approximation,” Eur. Control Conf. 2020, ECC 2020, pp. 1037–1042, 2020, doi: 10.23919/ecc51009.2020.9143625.
Other
Beginning: As soon as possible.
Duration: 3 month full time